
Category: mathematics

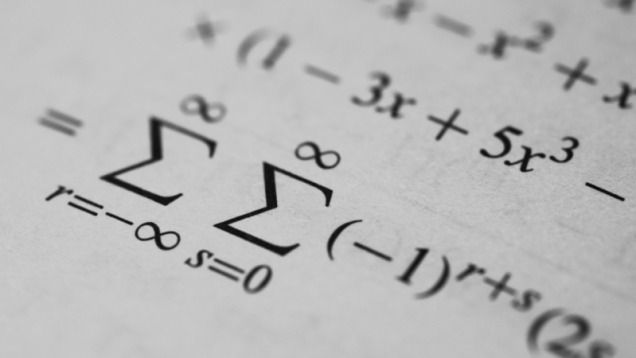
Mathematicians Discovered Something Super Freaky About Prime Numbers
Mathematicians have discovered a surprising pattern in the expression of prime numbers, revealing a previously unknown “bias” to researchers.
Primes, as you’ll hopefully remember from fourth-grade math class, are numbers that can only be divided by one or themselves (e.g. 2, 3, 5, 7, 11, 13, 17, etc.). Their appearance in the roll call of all integers cannot be predicted, and no magical formula exists to know when a prime number will choose to suddenly make an appearance. It’s an open question as to whether or not a pattern even exists, or whether or not mathematicians will ever crack the code of primes, but most mathematicians agree that there’s a certain randomness to the distribution of prime numbers that appear back-to-back.
Or at least that’s what they thought. Recently, a pair of mathematicians decided to test this “randomness” assumption, and to their shock, they discovered that it doesn’t actually exist. As reported in New Scientist, researchers Kannan Soundararajan and Robert Lemke Oliver of Stanford University in California have detected unexpected biases in the distribution of consecutive primes.

Kuiper Belt Objects Point The Way To Planet 9
On January 20th, 2016, researchers Konstantin Batygin and Michael E. Brown of Caltech announced that they had found evidence that hinted at the existence of a massive planet at the edge of the Solar System. Based on mathematical modeling and computer simulations, they predicted that this planet would be a super-Earth, two to four times Earth’s size and 10 times as massive. They also estimated that, given its distance and highly elliptical orbit, it would take 10,000 – 20,000 years to orbit the Sun.
Since that time, many researchers have responded with their own studies about the possible existence of this mysterious “Planet 9”. One of the latest comes from the University of Arizona, where a research team from the Lunar and Planetary Laboratory have indicated that the extreme eccentricity of distant Kuiper Belt Objects (KBOs) might indicate that they crossed paths with a massive planet in the past.


Astronomers estimate 100 billion habitable Earth-like planets in the Milky Way, 50 sextillion in the universe
Astronomers at the University of Auckland claim that there are actually around 100 billion habitable, Earth-like planets in the Milky Way — significantly more than the previous estimate of around 17 billion. There are roughly 500 billion galaxies in the universe, meaning there is somewhere in the region of 50,000,000,000,000,000,000,000 (5×10 22 ) habitable planets. I’ll leave you to do the math on whether one of those 50 sextillion planets has the right conditions for nurturing alien life or not.
The previous figure of 17 billion Earth-like planets in the Milky Way came from the Harvard-Smithsonian Center for Astrophysics in January, which analyzed data from the Kepler space observatory. Kepler essentially measures the dimming (apparent magnitude) of stars as planets transit in front of them — the more a star dims, the larger the planet. Through repeated observations we can work out the planet’s orbital period, from which we can usually derive the orbital distance and surface temperature. According to Phil Yock from the University of Auckland, Kepler’s technique generally finds “Earth-sized planets that are quite close to parent stars,” and are therefore “generally hotter than Earth [and not habitable].”
The University of Auckland’s technique, called gravitational microlensing, instead measures the number of Earth-size planets that orbit at twice the Sun-Earth distance. This results in a list of planets that are generally cooler than Earth — but by interpolating between this new list, and Kepler’s list, the Kiwi astronomers hope to generate a more accurate list of habitable, Earth-like planets. “We anticipate a number in the order of 100 billion,” says Yock.

Scott Aaronson On The Relevance Of Quantum Mechanics To Brain Preservation, Uploading, And Identity
Biography : Scott Aaronson is an Associate Professor of Electrical Engineering and Computer Science at MIT. His research interests center around the capabilities and limits of quantum computers, and computational complexity theory more generally. He also has written about consciousness and personal identity and the relevance of quantum mechanics to these issues.
Michael Cerullo: Thanks for taking the time to talk with me. Given the recent advances in brain preservation, questions of personal identity are moving from merely academic to extremely practical questions. I want to focus on your ideas related to the relevance of quantum mechanics to consciousness and personal identity which are found in your paper “Ghost in the Quantum Turing Machine” ( http://arxiv.org/abs/1306.0159 ), your blog “Could a Quantum Computer Have Subjective Experience?” ( http://www.scottaaronson.com/blog/?p=1951 ), and your book “Quantum Computing since Democritus” ( http://www.scottaaronson.com/democritus/) .
Before we get to your own speculations in this field I want to review some of the prior work of Roger Penrose and Stuart Hameroff ( http://www.quantumconsciousness.org/content/hameroff-penrose-review-orch-or-theory ). Let me try to summarize some of the criticism of their work (including some of your own critiques of their theory). Penrose and Hameroff abandon conventional wisdom in neuroscience (i.e. that neurons are the essential computational element in the brain) and instead posit that the microtubules (which conventional neuroscience tell us are involved in nucleic and cell division, organization of intracellular structure, and intracellular transport, as well as ciliary and flagellar motility) are an essential part of the computational structure of the brain. Specifically, they claim the microtubules are quantum computers that grant a person the ability to perform non-computable computations (and Penrose claims these kinds of computations are necessary for things like mathematical understanding). The main critiques of their theory are: it relies on future results in quantum gravity that don’t exist; there is no empirical evidence that microtubules are relevant to the function of the brain; work in quantum decoherence also makes it extremely unlikely that the brain is a quatum computer; even if a brain could somehow compute non-computable functions it isn’t clear what this has to do with consciousness. Would you say these are fair criticisms of their theory and are there any other criticisms you see as relevant?
Scott Aaronson: Yes, I think all four of those are fair criticisms! I could add a fifth criticism: Penrose’s case for the brain having non-computational abilities relies on an appeal to Gödel’s Incompleteness Theorem, to the idea that no machine working within a fixed formal system can prove the system’s consistency, whereas a human can “just see” that it’s consistent. But like most mathematicians and computer scientists, I don’t agree with that argument, because I think a machine could show all the same external behavior as a human who “sees” a formal system’s consistency. So then, the argument devolves into one about indescribable inner experiences, of “just seeing” (for example) that set theory is consistent. But if we wanted to rest the case on indescribable inner experiences, then why not forget about Gödel’s Theorem, and just talk about less abstruse things like the experience of falling in love or tasting strawberries or whatever?

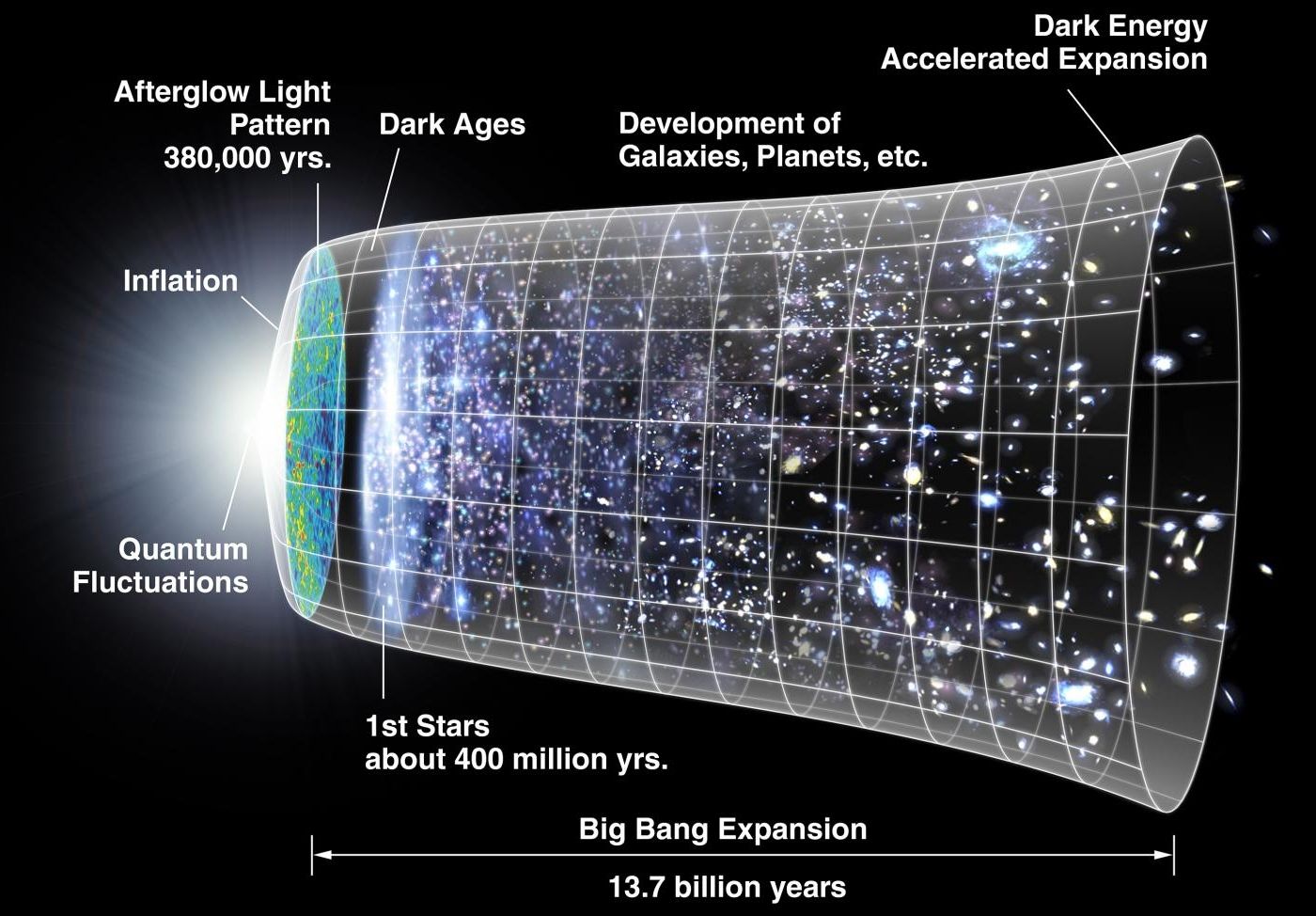
No Big Bang? Quantum equation predicts universe has no beginning
New equation proves no “Big Bang” theory and no beginning either as well as no singularity.
(Phys.org) —The universe may have existed forever, according to a new model that applies quantum correction terms to complement Einstein’s theory of general relativity. The model may also account for dark matter and dark energy, resolving multiple problems at once.
The widely accepted age of the universe, as estimated by general relativity, is 13.8 billion years. In the beginning, everything in existence is thought to have occupied a single infinitely dense point, or singularity. Only after this point began to expand in a “Big Bang” did the universe officially begin.
Although the Big Bang singularity arises directly and unavoidably from the mathematics of general relativity, some scientists see it as problematic because the math can explain only what happened immediately after—not at or before—the singularity.
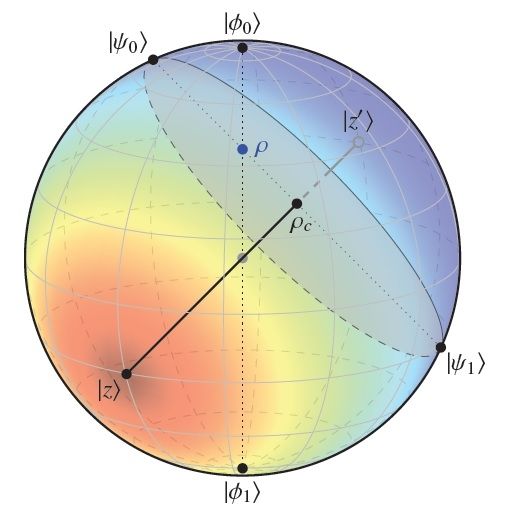
Physicists discover easy way to measure entanglement—on a sphere
Measuring entanglement — the amount of entanglement between states corresponds to the distance between two points on a Bloch sphere.
To do this, the scientists turned the difficult analytical problem into an easy geometrical one. They showed that, in many cases, the amount of entanglement between states corresponds to the distance between two points on a Bloch sphere, which is basically a normal 3D sphere that physicists use to model quantum states.
As the scientists explain, the traditionally difficult part of the math problem is that it requires finding the optimal decomposition of mixed states into pure states. The geometrical approach completely eliminates this requirement by reducing the many possible ways that states could decompose down to a single point on the sphere at which there is zero entanglement. The approach requires that there be only one such point, or “root,” of zero entanglement, prompting the physicists to describe the method as “one root to rule them all.”

The First Planet Discovered By Math
Two astronomers fought for credit when Neptune’s presence was confirmed in 1846: John Couch Adams from Britain, and Urbain Le Verrier from France. Both had used math and physics to predict Neptune’s position, but Le Verrier’s prediction turned out to be more accurate. See references.
