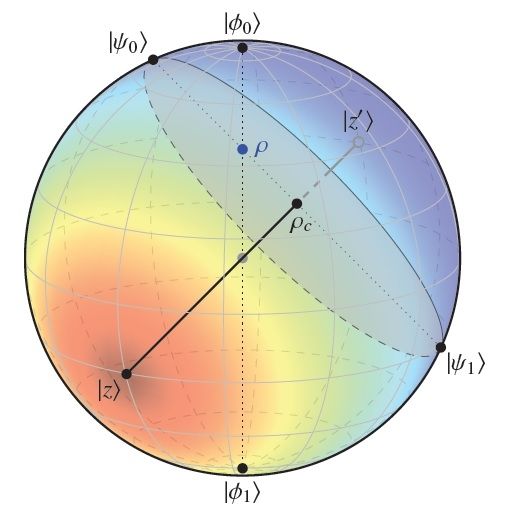
Measuring entanglement — the amount of entanglement between states corresponds to the distance between two points on a Bloch sphere.
To do this, the scientists turned the difficult analytical problem into an easy geometrical one. They showed that, in many cases, the amount of entanglement between states corresponds to the distance between two points on a Bloch sphere, which is basically a normal 3D sphere that physicists use to model quantum states.
As the scientists explain, the traditionally difficult part of the math problem is that it requires finding the optimal decomposition of mixed states into pure states. The geometrical approach completely eliminates this requirement by reducing the many possible ways that states could decompose down to a single point on the sphere at which there is zero entanglement. The approach requires that there be only one such point, or “root,” of zero entanglement, prompting the physicists to describe the method as “one root to rule them all.”