Lifeboat Foundation: Safeguarding Humanity
Toggle light / dark theme

Blog

Category: quantum physics

It’s always exciting when you can bridge two different physical concepts that seem to have nothing in common—and it’s even more thrilling when the results have as broad a range of possible fields of application as from fault-tolerant quantum computation to quantum gravity.

Physicists love to draw connections between distinct ideas, interconnecting concepts and theories to uncover new structure in the landscape of scientific knowledge. Put together information theory with quantum mechanics and you’ve opened a whole new field of quantum information theory. More recently, machine learning tools have been combined with many-body physics to find new ways to identify phases of matter, and ideas from quantum computing were applied to Pozner molecules to obtain new plausible models of how the brain might work.

In a recent contribution, my collaborators and I took a shot at combining the two physical concepts of quantum error correction and physical symmetries. What can we say about a quantum error-correcting code that conforms to a physical symmetry? Surprisingly, a continuous symmetry prevents the code from doing its job: A code can conform well to the symmetry, or it can correct against errors accurately, but it cannot do both simultaneously.

Read more | >

According to new research by SISSA, ICTP and INFN, black holes could be like holograms, in which all the information to produce a three-dimensional image is encoded in a two-dimensional surface. As affirmed by quantum theories, black holes could be incredibly complex, and concentrate an enormous amount of information in two dimensions, like the largest hard disks that exist in nature. This idea aligns with Einstein’s theory of relativity, which describes black holes as three dimensional, simple, spherical and smooth, as depicted in the first-ever image of a black hole that circulated in 2019. In short, black holes appear to be three dimensional, just like holograms. The study, which unites two discordant theories, has recently been published in Physical Review X.

The mystery of black holes

For scientists, pose formidable theoretical challenges for many reasons. They are, for example, excellent representatives of the great difficulties of theoretical physics in uniting the principles of Einstein’s general theory of relativity with those of the quantum physics of . According to the relativity, black holes are simple bodies without information. According to , as claimed by Jacob Bekenstein and Stephen Hawking, they are the most complex existing systems because they are characterized by enormous entropy, which measures the complexity of a system, and consequently contain a lot of information.

Read more | >

Technion Professor Ido Kaminer and his team have made a dramatic breakthrough in the field of quantum science: a quantum microscope that records the flow of light, enabling the direct observation of light trapped inside a photonic crystal.

Their research, “Coherent Interaction Between Free Electrons and a Photonic Cavity,” was published in Nature. All the experiments were performed using a unique ultrafast transmission electron microscope at the Technion-Israel Institute of Technology. The microscope is the latest and most versatile of a handful that exist in the scientific world.

“We have developed an electron microscope that produces, what is in many respects, the best near- field optical microscopy in the world. Using our microscope, we can change the color and angle of light that illuminates any sample of nano materials and map their interactions with electrons, as we demonstrated with photonic crystals,” explained Prof. Kaminer. “This is the first time we can actually see the dynamics of light while it is trapped in nano materials, rather than relying on ,” added Dr. Kangpeng Wang, a postdoc in the group and first author on the paper.

Read more | >

Learning quantum error correction: the image visualizes the activity of artificial neurons in the Erlangen researchers’ neural network while it is solving its task. © Max Planck Institute for the Science of Light.

Neural networks enable learning of error correction strategies for computers based on quantum physics

Quantum computers could solve complex tasks that are beyond the capabilities of conventional computers. However, the quantum states are extremely sensitive to constant interference from their environment. The plan is to combat this using active protection based on quantum error correction. Florian Marquardt, Director at the Max Planck Institute for the Science of Light, and his team have now presented a quantum error correction system that is capable of learning thanks to artificial intelligence.

Read more | >

A team of researchers at California Institute of Technology has found that arrays of strontium Rydberg atoms show promise for use in a quantum computer. In their paper published in the journal Nature Physics, the researchers describe their study of quantum entangled alkaline-earth Rydberg atoms arranged in arrays and what they learned about them. In the same issue, Wenhui Li, with the National University of Singapore, has published a News & Views piece exploring the state of quantum computing research, and outlines the work done by the team at CIT.

Quantum computers capable of conducting real computing work have still not been realized, but work continues as scientists are confident that the goal will be reached. And as Li notes, most of the early-stage demo quantum computers are based on or trapped ion platforms, though other systems are being studied, as well. One such system is based on in which the charges of the protons and electrons balance. In this new effort, the researchers looked at a type of neutral atom system based on Rydberg (excited atoms with one or more electrons that also have a high quantum number). To use such atoms in a quantum computer, they must, of course, be entangled—and there needs to be a lot of them, generally arranged in an array.

In their work, the team at CIT developed a way to demonstrate entanglement of Rydberg atoms in arrays—and as part of the system, they were able to detect and control Rydberg qubits with unprecedented fidelities. To achieve this feat, they began with realizing photon coupling between different levels of Rydberg ground-state qubits, thus avoiding scattering. Doing so also allowed for efficient detection of Rydberg states, greatly improving detection fidelity. The researchers also demonstrated two-qubit entanglement using tweezer potentials, also with .

Read more | >

Unprecedented View

The researchers believe this new nanoscale imaging technique could lead to the development of new materials and drugs, as well as the creation of better quantum computing systems.

“We can now see something that we couldn’t see before,” researcher Christopher Lutz told The New York Times. “So our imagination can go to a whole bunch of new ideas that we can test out with this technology.”

Read more | >

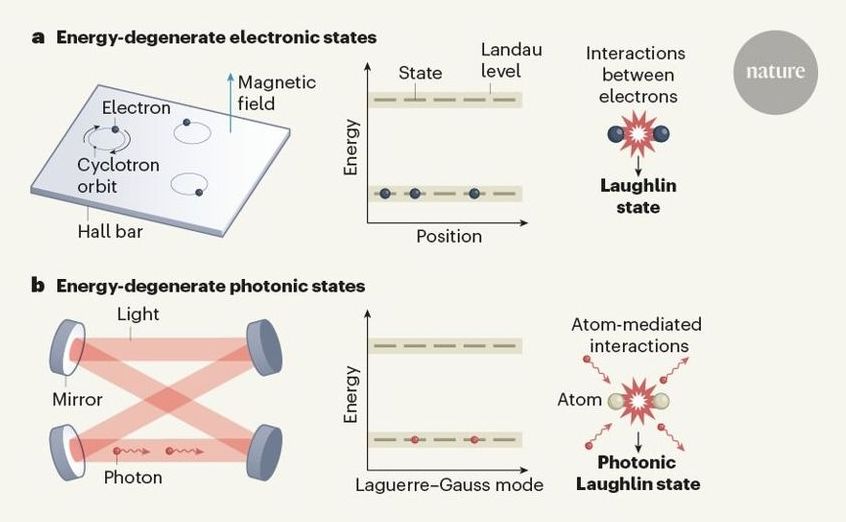
Solving a difficult physics problem can be surprisingly similar to assembling an interlocking mechanical puzzle. In both cases, the particles or pieces look alike, but can be arranged into a beautiful structure that relies on the precise position of each component (Fig. 1). In 1983, the physicist Robert Laughlin made a puzzle-solving breakthrough by explaining the structure formed by interacting electrons in a device known as a Hall bar1. Although the strange behaviour of these electrons still fascinates physicists, it is not possible to simulate such a system or accurately measure the particles’ ultrashort time and length scales. Writing in Nature, Clark et al.2 report the creation of a non-electronic Laughlin state made of composite matter–light particles called polaritons, which are easier to track and manipulate than are electrons.

To picture a Laughlin state, consider a Hall bar, in which such states are usually observed (Fig. 2a). In these devices, electrons that are free to move in a two-dimensional plane are subjected to a strong magnetic field perpendicular to the plane. In classical physics, an electron at any position will start moving along a circular trajectory known as a cyclotron orbit, the radius of which depends on the particle’s kinetic energy. In quantum mechanics, the electron’s position will still be free, but its orbital radius — and, therefore, its kinetic energy — can be increased or decreased only in discrete steps. This feature leads to large sets of equal-energy (energy-degenerate) states called Landau levels. Non-interacting electrons added to the lowest-energy Landau level can be distributed between the level’s energy-degenerate states in many different ways.

Adding repulsive interactions between the electrons constrains the particles’ distribution over the states of the lowest Landau level, favouring configurations in which any two electrons have zero probability of being at the same spot. The states described by Laughlin have exactly this property and explain the main features of the fractional quantum Hall effect, whereby electrons in a strong magnetic field act together to behave like particles that have fractional electric charge. This work earned Laughlin a share of the 1998 Nobel Prize in Physics. Laughlin states are truly many-body states that cannot be described by typical approximations, such as the mean-field approximation. Instead, the state of each particle depends on the precise state of all the others, just as in an interlocking puzzle.

Read more | >

Government agencies and universities around the world—not to mention tech giants like IBM and Google—are vying to be the first to answer a trillion-dollar quantum question : How can quantum computers reach their vast potential when they are still unable to consistently produce results that are reliable and free of errors?

Every aspect of these exotic machines—including their fragility and engineering complexity; their preposterously sterile, low-temperature operating environment; complicated mathematics; and their notoriously shy quantum bits (qubits) that flip if an operator so much as winks at them—are all potential sources of errors. It says much for the ingenuity of scientists and engineers that they have found ways to detect and correct these errors and have quantum computers working to the extent that they do: at least long enough to produce limited results before errors accumulate and quantum decoherence of the qubits kicks in.

Read more | >