Conway, who passed away on April 11, was known for his rapid computation, his playful approach, and solving problems with “his own bare hands.”


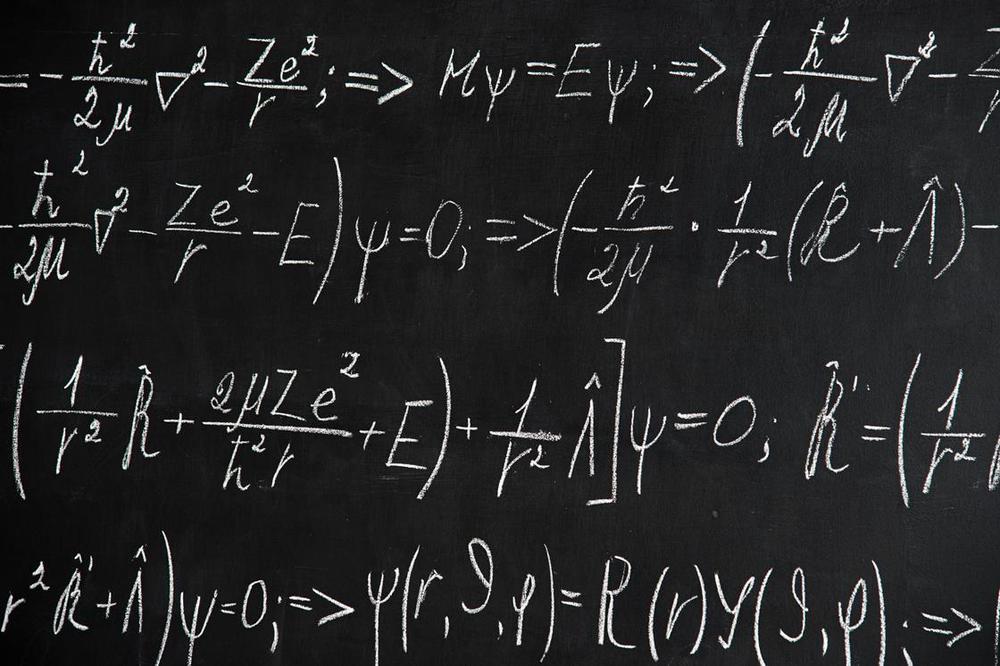
Using machine learning three groups, including researchers at IBM and DeepMind, have simulated atoms and small molecules more accurately than existing quantum chemistry methods. In separate papers on the arXiv preprint server the teams each use neural networks to represent wave functions of electrons that surround the molecules’ atoms. This wave function is the mathematical solution of the Schrödinger equation, which describes the probabilities of where electrons can be found around molecules. It offers the tantalising hope of ‘solving chemistry’ altogether, simulating reactions with complete accuracy. Normally that goal would require impractically large amounts of computing power. The new studies now offer a compromise of relatively high accuracy at a reasonable amount of processing power.
Each group only simulates simple systems, with ethene among the most complex, and they all emphasise that the approaches are at their very earliest stages. ‘If we’re able to understand how materials work at the most fundamental, atomic level, we could better design everything from photovoltaics to drug molecules,’ says James Spencer from DeepMind in London, UK. ‘While this work doesn’t achieve that quite yet, we think it’s a step in that direction.’
Two approaches appeared on arXiv just a few days apart in September 2019, both combining deep machine learning and Quantum Monte Carlo (QMC) methods. Researchers at DeepMind, part of the Alphabet group of companies that owns Google, and Imperial College London call theirs Fermi Net. They posted an updated preprint paper describing it in early March 2020.1 Frank Noé’s team at the Free University of Berlin, Germany, calls its approach, which directly incorporates physical knowledge about wave functions, PauliNet.2


John Horton Conway, a legendary mathematician who stood out for his love of games and for bringing mathematics to the masses, died on Saturday, April 11, in New Brunswick, New Jersey, from complications related to COVID-19. He was 82.
Known for his unbounded curiosity and enthusiasm for subjects far beyond mathematics, Conway was a beloved figure in the hallways of Princeton’s mathematics building and at the Small World coffee shop on Nassau Street, where he engaged with students, faculty and mathematical hobbyists with equal interest.
Conway, who joined the faculty in 1987, was the John von Neumann Professor in Applied and Computational Mathematics and a professor of mathematics until 2013 when he transferred to emeritus status.

The devil staircase findings.
April 14 (UPI) — The timing of large, shallow earthquakes across the globe follows a mathematical pattern known as the devil’s staircase, according to a new study of seismic sequences.
Previously, scientists and their models have theorized that earthquake sequences happen periodically or quasi-periodically, following cycles of growing tension and release. Researchers call it the elastic rebound model. In reality, periodic earthquake sequences are surprisingly rare.
Instead, scientists found global earthquake sequences tend to occur in clusters — outbursts of seismic events separated by long but irregular intervals of silence.

If anyone wants to learn about the future of artificial intelligence and the rise of super-intelligent machines here is Billionaire rocket scientist businessman Elon Musk’s favorite book of the year written by MIT math Professor Max Tegmark at the Future of Life Institute. The book Life 3.0 is presented in this free audio-book format on YouTube and is a 7 hour video talking about how we will become a Libertarian Utopia soon thanks to advances in technology.

At the regional level and worldwide, the occurrence of large shallow earthquakes appears to follow a mathematical pattern called the Devil’s Staircase, where clusters of earthquake events are separated by long but irregular intervals of seismic quiet.
The finding published in the Bulletin of the Seismological Society of America differs from the pattern predicted by classical earthquake modeling that suggests earthquakes would occur periodically or quasi-periodically based on cycles of build-up and release of tectonic stress. In fact, say Yuxuan Chen of the University of Missouri, Columbia, and colleagues, periodic large earthquake sequences are relatively rare.
The researchers note that their results could have implications for seismic hazard assessment. For instance, they found that these large earthquake sequences (those with events magnitude 6.0 or greater) are “burstier” than expected, meaning that the clustering of earthquakes in time results in a higher probability of repeating seismic events soon after a large earthquake. The irregular gap between event bursts also makes it more difficult to predict an average recurrence time between big earthquakes.

Has one of the major outstanding problems in number theory finally been solved? Or is the 600-page proof missing a key piece? The verdict isn’t in yet, but the proof, at least, will finally appear in a peer-reviewed journal.
However, there’s just one catch: the mathematician himself, Shinichi Mochizuki, is one of the journal’s seniormost editors.
Nowadays, artificial neural networks have an impact on many areas of our day-to-day lives. They are used for a wide variety of complex tasks, such as driving cars, performing speech recognition (for example, Siri, Cortana, Alexa), suggesting shopping items and trends, or improving visual effects in movies (e.g., animated characters such as Thanos from the movie Infinity War by Marvel).
Traditionally, algorithms are handcrafted to solve complex tasks. This requires experts to spend a significant amount of time to identify the optimal strategies for various situations. Artificial neural networks — inspired by interconnected neurons in the brain — can automatically learn from data a close-to-optimal solution for the given objective. Often, the automated learning or “training” required to obtain these solutions is “supervised” through the use of supplementary information provided by an expert. Other approaches are “unsupervised” and can identify patterns in the data. The mathematical theory behind artificial neural networks has evolved over several decades, yet only recently have we developed our understanding of how to train them efficiently. The required calculations are very similar to those performed by standard video graphics cards (that contain a graphics processing unit or GPU) when rendering three-dimensional scenes in video games.