Lifeboat Foundation: Safeguarding Humanity
Toggle light / dark theme

Blog

Category: quantum physics

The present essay is the third of a group of four communications originally intended for publication in Infinite Energy at Dr. Eugene Mallove’s invitation, and dedicated to the scientific, technological and political problems presented by exotic flight and lift systems in particular those relating to possible control of gravity. We examine the main lines of research into the nature of gravity over the past 6 decades, with a focus on Einstein’s General Relativity and General Theory of Gravitation, quantum-mechanical models of the graviton, Geometrodynamics and the ZPE theories, Van Flandern’s model of gravity, which are contrasted to Aspden’s theory of a dynamic Aetherometric Theory of Synchronicity, Vol. II AS3-II.9.

Read more | >

From the fictional universe of Stargate Atlantis and Marvel Comic’s Realm of Kings to NASA’s Eagleworks Propulsion laboratory, zero-point energy, also known as vacuum energy, is touted as a potentially limitless and ubiquitous source of energy, if one can only find the means to harness it. [1] Zero-point energy can be formulated in a few different ways, but in its most basic form, it is the minimal yet non-zero energy of a quantum mechanical system. In quantum field theory, zero-point energy can be considered by computing the expected energy of the zero photon mode. [2] In a system with no physical boundaries, the expected energy of the zero photon mode diverges! Yet, if this energy uniformly permeates all of space-time, it is not directly observable.

Conceptual Framework

For pedagogical reasons, we will consider the popular formulation of zero-point energy. The most interesting and relevant framework for zero-point energy can be understood from the quantum field theory for photons and electrons: quantum electrodynamics. Glossing over an exceptional amount of mathematical and conceptual background, the energy of a state in quantum field theory is computed as an expectation of a Hamiltonian„ which describes the energy of the state in terms of operators acting on wavefunctions. The final computation usually requires an integral over the allowed momenta of particles in the state.

Read more | >

Quantum gauge theories are mathematical constructs that are typically used by physicists to describe subatomic particles, their associated wave fields and the interactions between them. The dynamics outlined by these theories are difficult to compute, yet effectively emulating them in the lab could lead to valuable new insight and discoveries.

In a recent study, a team of researchers at ETH Zurich’s Institute for Quantum Electronics successfully implemented a fundamental ingredient for the simulation of quantum gauge theories in a laboratory experiment. Their hope is that by simulating in a highly controlled environment, they will gather interesting observations and broaden their understanding of many-body systems (i.e., systems with many particles that interact with each other).

“Usually, our work is inspired by phenomena in solid state physics such as strongly correlated phases of electrons in complex materials,” Tilman Esslinger, one of the researchers who carried out the study, told Phys.org. “In our current work, however, we wanted to extend the scope of our experimental platform (i.e., in optical lattices) in order to investigate a new set of phenomena occurring in high-energy and condensed matter physics. The objective was to demonstrate that it is possible to engineer gauge fields in our setup that are dynamical quantum degrees of freedom due to their coupling to a matter field.”

Read more | >

Quantum information relies on the possibility of writing messages in a quantum particle and reading them out in a reliable way. If, however, the particle is relativistic, meaning that it moves with velocities close to the speed of light, it is impossible for standard techniques to decode the message unambiguously, and the communication therefore fails.

Thanks to the introduction of a new method, researchers at the University of Vienna and the Austrian Academy of Sciences have developed reliable decoding of quantum messages transmitted at extremely . The results, published in the journal Physical Review Letters, opens up new possibilities of technological applications in and quantum communication.

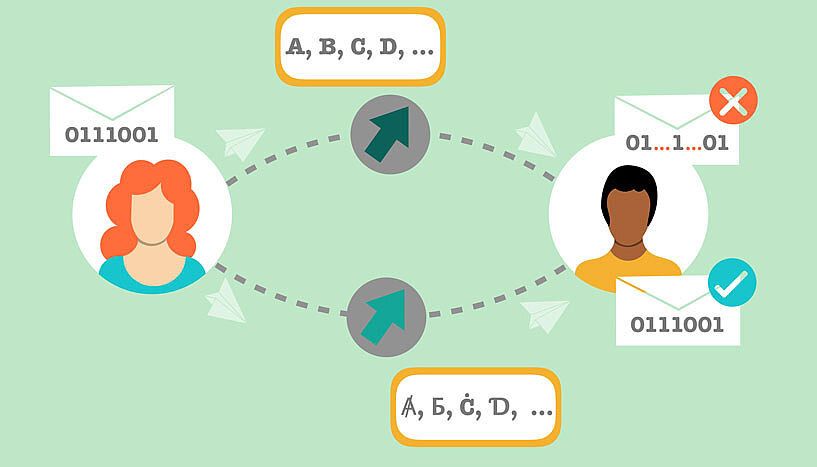
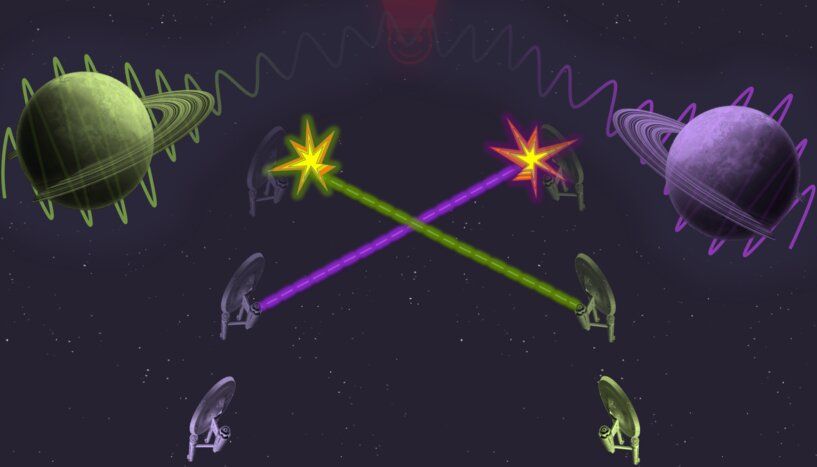
Imagine the following situation: Anna and Bill want to exchange a message by using a property of a , say the spin of an electron, which is an intrinsic form of particle’s rotation. Bill needs Anna’s message as quickly as possible, so Anna has to send the electron at maximum speed, very close to the speed of light. Given that Anna has the electron in her laboratory localized, the Heisenberg uncertainty principle forbids the velocity of the electron to be defined with arbitrary precision. When the electron travels at extremely high , the interplay between special relativity and quantum physics causes the spin and the velocity of the electron to become entangled. Due to this correlation, which is stronger than what is classically possible, Bill is not able to read out the spin with the standard method. Can Anna and Bill improve their communication strategy?

Read more | >

The theories of quantum mechanics and gravity are notorious for being incompatible, despite the efforts of scores of physicists over the past fifty years. However, recently an international team of researchers led by physicists from the University of Vienna, the Austrian Academy of Sciences as well as the University of Queensland (AUS) and the Stevens Institute of Technology (U.S.) have combined the key elements of the two theories describing the flow of time and discovered that temporal order between events can exhibit genuine quantum features.

According to general relativity, the presence of a slows down the flow of time. This means that a clock placed close to a massive object will run slower as compared to an identical one that is further away.

However, the rules of quantum theory allow for any object to be prepared in a . A superposition state of two locations is different to placing an object in one or the other location randomly—it is another way for an object to exist, allowed by the laws of quantum physics.

Read more | >

Circa 1997

By Michio Kaku

IS THERE a Final Theory in physics? Will we one day have a complete theory that will explain everything from subatomic particles, atoms and supernovae to the big bang? Einstein spent the last 30 years of his life in a fruitless quest for the fabled unified field theory. His approach has since been written off as futile.

In the 1980s, attention switched to superstring theory as the leading candidate for a final theory. This revolution began when physicists realised that the subatomic particles found in nature, such as electrons and quarks, may not be particles at all, but tiny vibrating strings.

Read more | >

We suggest and motivate a precise equivalence between uncompactified eleven dimensional M-theory and the N = infinity limit of the supersymmetric matrix quantum mechanics describing D0-branes. The evidence for the conjecture consists of several correspondences between the two theories. As a consequence of supersymmetry the simple matrix model is rich enough to describe the properties of the entire Fock space of massless well separated particles of the supergravity theory. In one particular kinematic situation the leading large distance interaction of these particles is exactly described by supergravity.

The model appears to be a nonperturbative realization of the holographic principle. The membrane states required by M-theory are contained as excitations of the matrix model.

Read more | >