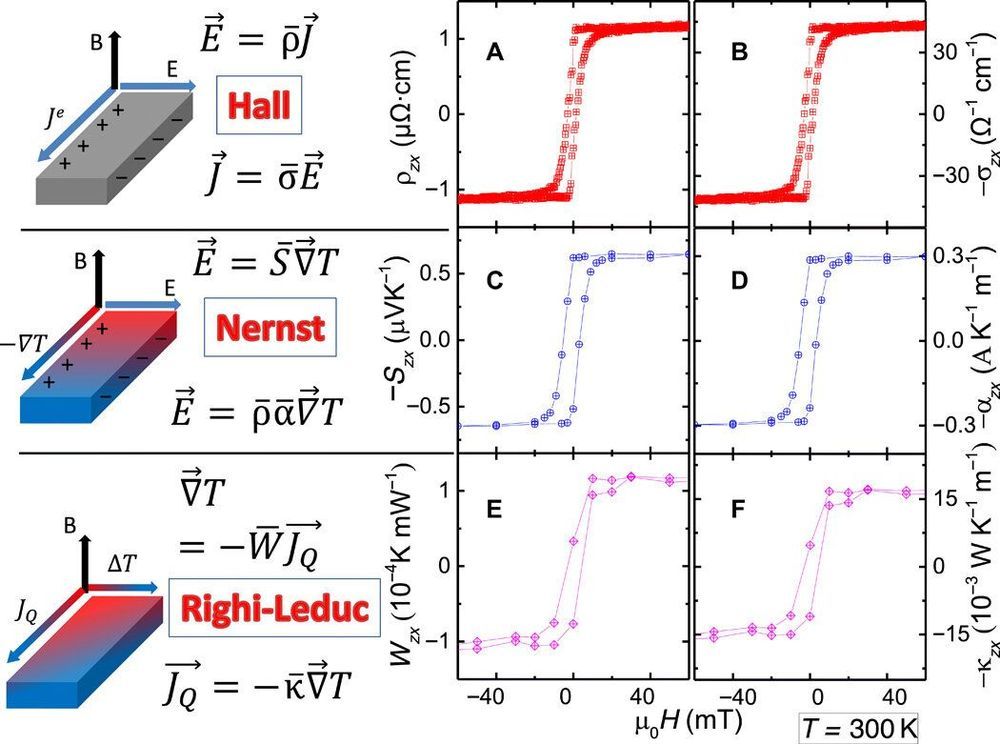
According to the Wiedemann-Franz (WF) law, the electrical conductivity of a metal is linked to its thermal counterpart, provided that the heat carried by the phonons is negligible and the electrons do not suffer inelastic scattering. In a type II Weyl semimetal also known as a fourth fermion, the thermal dependence of the ratio between electrical and thermal conductivity highlights deviations from the Wiedemann-Franz law. Physicists have tested the WF law in numerous solids but intend to understand the extent of its relevance during anomalous transverse transport and investigate the topological nature of the wave function. In a new report, Liangcai Xu and an international research team in condensed matter physics in China, France, Israel and Germany, presented a study of the anomalous transverse response in a noncollinear antiferromagnetic Weyl semimetal, Mn₃Ge. They varied the experimental conditions from room temperature down to sub-Kelvin temperature and observed finite-temperature violation of the WF correlation. They credited the outcome to a mismatch between the thermal and electrical summations of the Berry curvature (a geometric phase acquired within the course of a cycle) and not due to inelastic scattering. The team backed their interpretation with theoretical calculations to reveal a competition between the temperature and Berry curvature distribution. The work is now published on Science Advances.

The Berry curvature of electrons can result in the anomalous Hall effect (AHE) if the host solid lacks time-reversal symmetry (conservation of entropy). While the thermoelectric and thermal counterparts of the anomalous Hall effect are explored less frequently, they too arise from the same fictitious magnetic fields. It remains to be determined how the magnitudes of such anomalous off-diagonal coefficients correlate with each other and if the established correlations between ordinary transport coefficients continue to hold. It is currently laborious to form a semiclassical formula of the anomalous Hall effect (AHE), thereby making any intuitive picture of producing a transverse electric field even more challenging. In this work, the research team presented a study of a magnetic solid, focused on the relation between anomalous electrical and thermal Hall conductivities. Xu et al.