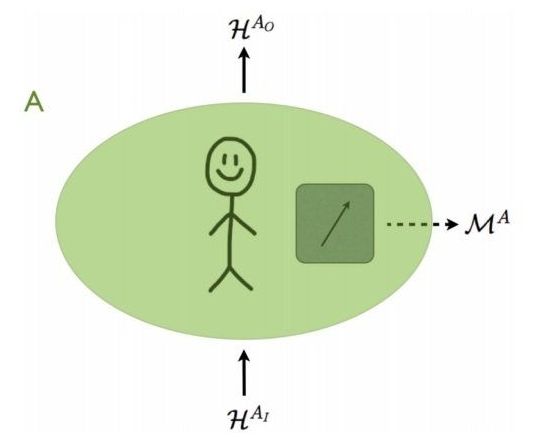
Quantum theory is based heavily on probabilities, since measuring a quantum system doesn’t produce the same outcome every time, but instead yields one of many outcomes that each occur with a certain probability. Now in a new paper, physicists have presented a new quantum probability rule for assigning probabilities to measurement outcomes, or events, that essentially combines two of the most important quantum probability rules (the Born rule and the wave function collapse rule) into one.
The physicists, Sally Shrapnel, Fabio Costa, and Gerard Milburn, at The University of Queensland in Australia, have published a paper on the new quantum probability rule in the New Journal of Physics.
One of the most important probability rules in quantum theory is the Born rule, which gives the probability that a measurement yields a certain event. However, things get a little bit more complicated when predicting consecutive events. Although in classical scenarios it’s possible to assign joint probabilities to consecutive events using conditioning, in quantum scenarios this is not possible since each measurement necessarily disturbs the system. So in quantum mechanics, the state must be updated with this new information after every measurement.