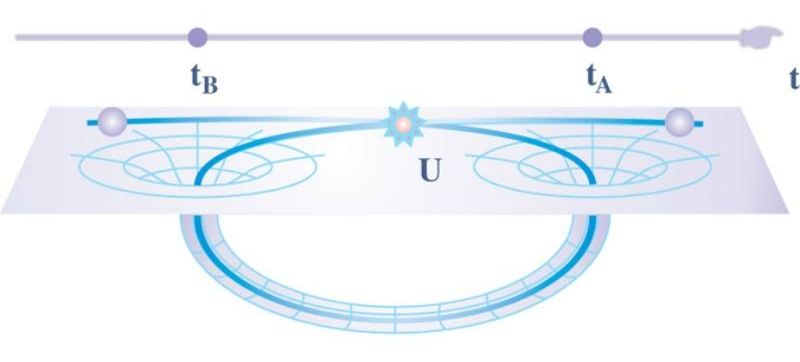
In general relativity, closed timelike curves can break causality with remarkable and unsettling consequences. At the classical level, they induce causal paradoxes disturbing enough to motivate conjectures that explicitly prevent their existence. At the quantum level such problems can be resolved through the Deutschian formalism, however this induces radical benefits—from cloning unknown quantum states to solving problems intractable to quantum computers. Instinctively, one expects these benefits to vanish if causality is respected. Here we show that in harnessing entanglement, we can efficiently solve NP-complete problems and clone arbitrary quantum states—even when all time-travelling systems are completely isolated from the past. Thus, the many defining benefits of Deutschian closed timelike curves can still be harnessed, even when causality is preserved. Our results unveil a subtle interplay between entanglement and general relativity, and significantly improve the potential of probing the radical effects that may exist at the interface between relativity and quantum theory.