One of the main principles of quantum physics is the superposition of states. Systems are simultaneously in different states, i.e. “alive and dead” at the same time such as Schrödinger’s cat, until someone measures them and the system opts for one of the possibilities. As long as the superposition lasts the system is said to be in a coherent state. In real systems, sets of diverse elemental particles or atoms existing in a state of superposition, for example, in different positions simultaneously, with different levels of energy, or with two opposite spin orientations, have weak coherence: the superposition is broken easily by the vibrations associated with temperature and the interactions with the environment.
In the scientific article, researchers from the Universitat Autònoma de Barcelona Department of Physics Andreas Winter and Dong Yang propose a groundbreaking method with which to measure the degree of coherence in any given quantum state. The researchers created simple formulas to calculate how much “pure coherence” is contained in a given quantum state, by answering two fundamental questions: How efficiently can one transform the state into “pure coherence”? And how efficient is the reverse process?
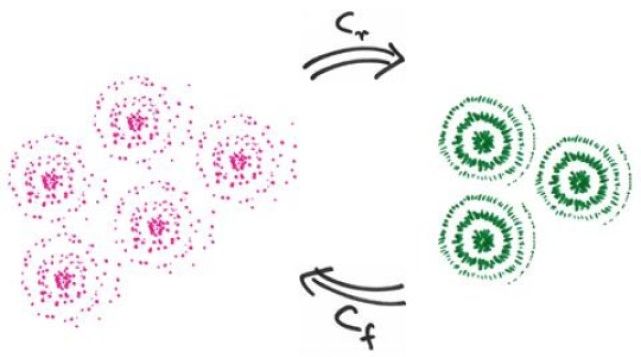
“At first the quantum state must be distilled. We must see how much coherence can be extracted from it,” explains Andreas Winter, to later “once again form a noisy state in which the coherence is diluted.” The distillation and dilution process allows measuring the strength of coherence of the initial state of superposition with experiments which can be tailored to each particular case. This is an outstanding contribution to the study of quantum physics given that “traditionally, to measure the degree of coherence of a superposition it was necessary to be able to measure the visibility of interference fringes, linked to standardised experiments,” Winter highlights. “With our approach, in contrast, the experiment can be adapted to every state in order to make the quantum coherence manifest itself better.”