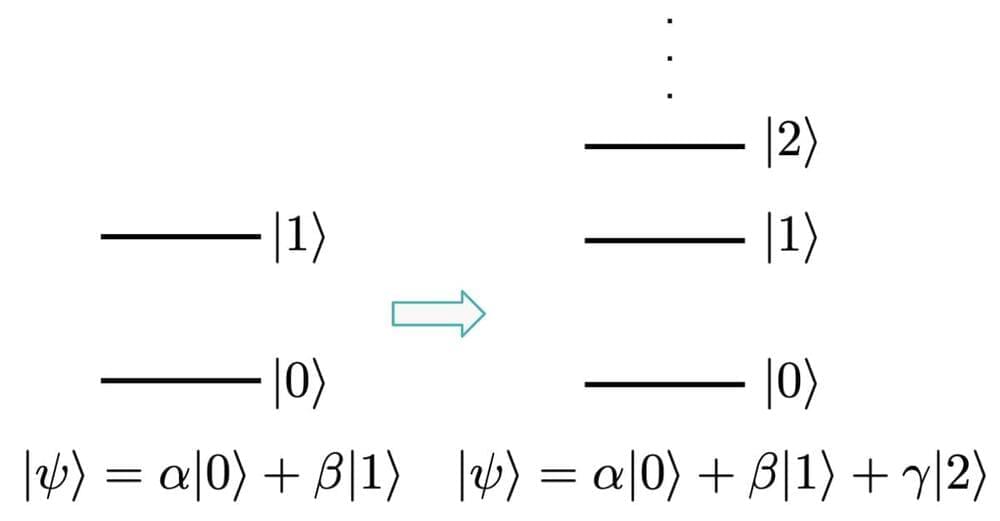By Alex Hill, Senior Quantum Systems Engineer

Qubits are the basic building block of a quantum processor, and are so named because they represent a continuum of complex superpositions of two basic quantum states. The power of qubits comes in part from their ability to encode significantly more information than a classical bit — an infinite set of states between 0 and 1. In mathematical terms, quantum gates that manipulate the state of individual qubits are unitary operators drawn from SU.

Rigetti’s superconducting quantum processors are based on the transmon design [1]. Each physical qubit is an anharmonic oscillator, meaning that the energy gaps between subsequent qubit energy states decrease as the qubit climbs higher up the state ladder. We typically only address the first two states, 0 and 1 (in the literature, sometimes referred to as g(round) and e(xcited)); however, the design of our qubits supports even higher states. The simple structure of the transmon energy levels gives superconducting qubits the unique ability to address many of these states in a single circuit.