By Stina Andersson and Ellinor Wanzambi

Researchers have been working on quantum algorithms since physicists first proposed using principles of quantum physics to simulate nature decades. One important component in many quantum algorithms is quantum walks, which are the quantum equivalent of the classical Markov chain, i.e., a random walk without memory. Quantum walks are used in algorithms in areas such as searching, node ranking in networks, and element distinctness.

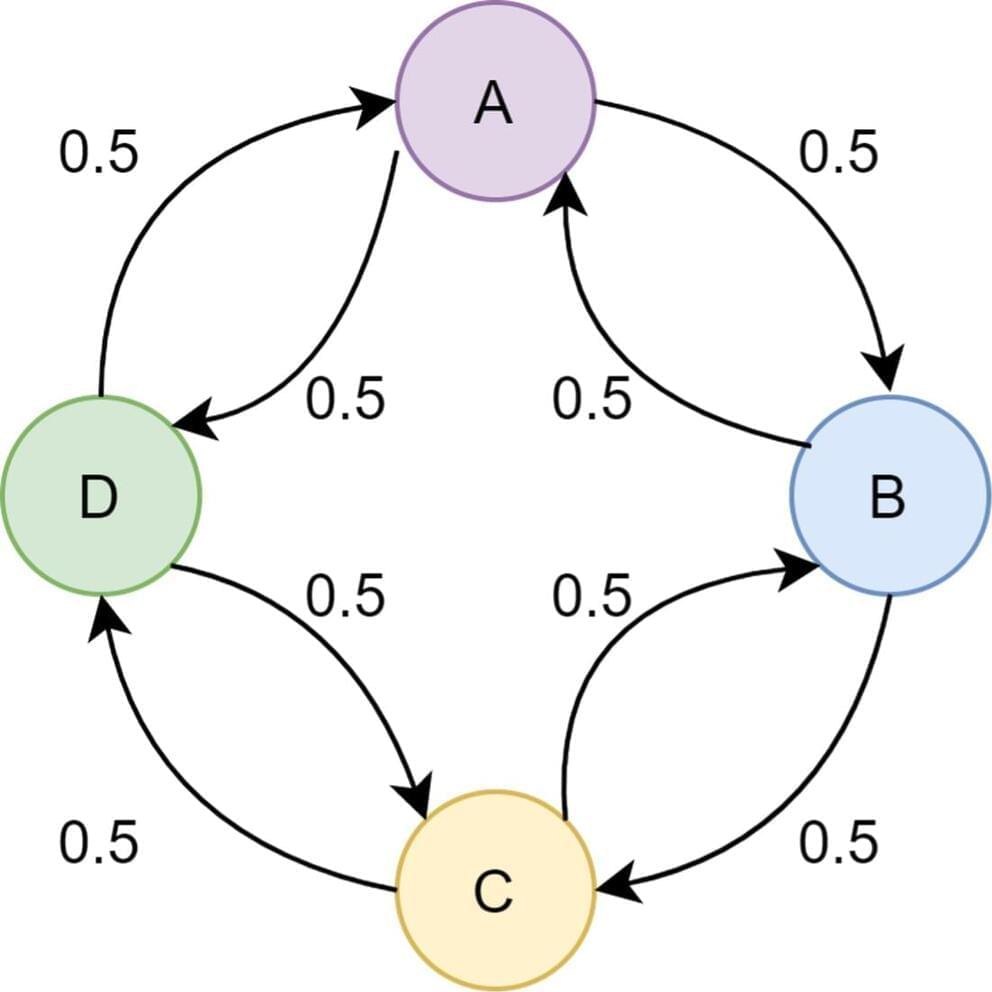
Consider the graph in Figure 1 and imagine that we randomly want to move between nodes A, B, C, and D in the graph. We can only move between nodes that are connected by an edge, and each edge has an associated probability that decides how likely we are to move to the connected node. This is a random walk. In this article, we are working only with Markov chains, also called the memory-less random walks, meaning that the probabilities are independent of the previous steps. For example, the probabilities of arriving at node A are the same no matter if we got there from node B or node D.